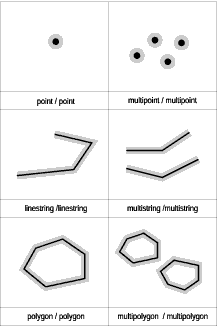
The preceding sections introduced three categories of spatial functions:
This section introduces three more categories:
Several spatial functions return information about ways in which geographic features relate to one another or compare with one another. Most of these functions, called predicates, are boolean functions. This section describes the predicates in general and then discusses each function individually.
Predicate functions return 1 (TRUE) if a comparison meets the function's criteria, or 0 (FALSE) if the comparison fails. Predicates that test for a spatial relationship compare pairs of geometries that can be a different type or dimension.
Predicates compare the X and Y coordinates of the submitted geometries. The Z coordinates and the measure (if they exist) are ignored. This allows geometries that have Z coordinates or measure to be compared with those that do not.
The Dimensionally Extended 9 Intersection Model (DE-9IM) 1 is a mathematical approach that defines the pair-wise spatial relationship between geometries of different types and dimensions. This model expresses spatial relationships between all types of geometries as pair-wise intersections of their interior, boundary and exterior, with consideration for the dimension of the resulting intersections.
Given geometries a and b: I(a ), B(a ), and E(a ) represent the interior, boundary, and exterior of a. And, I(b), B(b), and E(b) represent the interior, boundary, and exterior of b. The intersections of I(a), B(a), and E(a) with I(b), B(b), and E(b) produces a 3 by 3 matrix. Each intersection can result in geometries of different dimensions. For example, the intersection of the boundaries of two polygons consists of a point and a linestring, in which case the dim function would return the maximum dimension of 1.
The dim function returns a value of 1, 0, 1 or 2. The 1 corresponds
to the null set or dim(null), which is returned when no intersection was
found.
|
|
Interior
|
Boundary
|
Exterior
|
|
Interior
|
dim(I(a) &intersect. I(b))
|
dim(I(a) &intersect. B(b))
|
dim(I(a) &intersect. E(b))
|
|
Boundary
|
dim(B(a) &intersect. I(b))
|
dim(B(a) &intersect. B(b))
|
dim(B(a) &intersect. E(b))
|
|
Exterior
|
dim(E(a) &intersect. I(b))
|
dim(E(a) &intersect. B(b))
|
dim(E(a) &intersect. E(b))
|
The results of the spatial relationship predicates can be understood or verified by comparing the results of the predicate with a pattern matrix that represents the acceptable values for the DE-9IM.
The pattern matrix contains the acceptable values for each of the intersection matrix cells. The possible pattern values are:
For example, the following pattern matrix for the ST_Within predicate
includes the values T, F, and *.
Table 40. Matrix for ST_Within
| The pattern matrix of the ST_Within predicate for geometry combinations. | ||||
|
|
|
b
|
|
|
|
|
|
Interior
|
Boundary
|
Exterior
|
|
a
|
Interior
|
T
|
*
|
F
|
|
|
Boundary
|
*
|
*
|
F
|
|
|
Exterior
|
*
|
*
|
*
|
The ST_Within predicate returns TRUE when the interiors of both geometries intersect and when the interior and boundary of a does not intersect the exterior of b. All other conditions do not matter.
Each predicate has at least one pattern matrix, but some require more than one to describe the relationships of various geometry type combinations.
ST_Equals returns 1 (TRUE) if two geometries of the same type have identical X,Y coordinate values.
Figure 14. ST_Equals. Geometries are equal if they have matching X,Y coordinates.
 |
| The DE-9IM pattern matrix for equality ensures that the interiors intersect and that no part interior or boundary of either geometry intersects the exterior of the other. | ||||
|
|
|
b
|
|
|
|
|
|
Interior
|
Boundary
|
Exterior
|
|
a
|
Interior
|
T
|
*
|
F
|
|
|
Boundary
|
*
|
*
|
F
|
|
|
Exterior
|
F
|
F
|
*
|
For more information, see ST_Equals.
ST_OrderingEquals compares two geometries and returns 1 (TRUE) if the geometries are equal and the coordinates are in the same order; otherwise, it returns 0 (FALSE). For more information, see ST_OrderingEquals.
ST_Disjoint returns 1 (TRUE) if the intersection of the two geometries is an empty set.
Figure 15. ST_Disjoint. Geometries are disjoint if they do not intersect one another in any way.
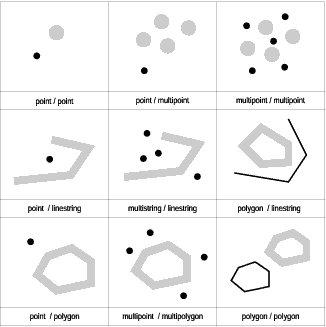 |
Table 42. Matrix for ST_Disjoint
| The ST_Disjoint predicate's pattern matrix simple states that neither the interiors nor the boundaries of either geometry intersect. | ||||
|
|
|
b
|
|
|
|
|
|
Interior
|
Boundary
|
Exterior
|
|
a
|
Interior
|
F
|
F
|
*
|
|
|
Boundary
|
F
|
F
|
*
|
|
|
Exterior
|
*
|
*
|
*
|
For more information, see ST_Disjoint.
ST_Intersects returns 1 (TRUE) if the intersection does not result in an empty set. Intersects returns the exact opposite result of ST_Disjoint.
The ST_Intersects predicate returns TRUE if the conditions of any of the
following pattern matrices returns TRUE.
Table 43. Matrix for ST_Intersects (1)
| The ST_Intersects predicate returns TRUE if the interiors of both geometries intersect. | ||||
|
|
|
b
|
|
|
|
|
|
Interior
|
Boundary
|
Exterior
|
|
a
|
Interior
|
T
|
*
|
*
|
|
|
Boundary
|
*
|
*
|
*
|
|
|
Exterior
|
*
|
*
|
*
|
Table 44. Matrix for ST_Intersects (2)
| The ST_Intersects predicate returns TRUE if the boundary of the first geometry intersects the boundary of the second geometry. | ||||
|
|
|
b
|
|
|
|
|
|
Interior
|
Boundary
|
Exterior
|
|
a
|
Interior
|
*
|
T
|
*
|
|
|
Boundary
|
*
|
*
|
*
|
|
|
Exterior
|
*
|
*
|
*
|
Table 45. Matrix for ST_Intersects (3)
| The ST_Intersects predicate returns TRUE if the boundary of the first geometry intersects the interior of the second. | ||||
|
|
|
b
|
|
|
|
|
|
Interior
|
Boundary
|
Exterior
|
|
a
|
Interior
|
*
|
*
|
*
|
|
|
Boundary
|
T
|
*
|
*
|
|
|
Exterior
|
*
|
*
|
*
|
Table 46. Matrix for ST_Intersects (4)
| The ST_Intersects predicate returns TRUE if the boundaries of either geometry intersect. | ||||
|
|
|
b
|
|
|
|
|
|
Interior
|
Boundary
|
Exterior
|
|
a
|
Interior
|
*
|
*
|
*
|
|
|
Boundary
|
*
|
T
|
*
|
|
|
Exterior
|
*
|
*
|
*
|
For more information, see ST_Intersects.
This function returns 1 (TRUE) if the envelopes of two geometries intersect. It is a convenience function that efficiently implements ST_Intersects (ST_Envelope(g1),ST_Envelope(g2)). For more information, see EnvelopesIntersect.
ST_Touches returns 1 (TRUE) if none of the points common to both geometries intersect the interiors of both geometries. At least one geometry must be a linestring, polygon, multilinestring or multipolygon.
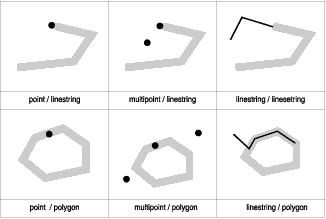 |
The pattern matrices show that the ST_Touches predicate returns TRUE when
the interiors of the geometry do not intersect, and the boundary of either
geometry intersects the other's interior or its boundary.
Table 47. Matrix for ST_Touches (1)
|
|
|
b
|
|
|
|
|
|
Interior
|
Boundary
|
Exterior
|
|
a
|
Interior
|
F
|
T
|
*
|
|
|
Boundary
|
*
|
*
|
*
|
|
|
Exterior
|
*
|
*
|
*
|
Table 48. Matrix for ST_Touches (2)
|
|
|
b
|
|
|
|
|
|
Interior
|
Boundary
|
Exterior
|
|
a
|
Interior
|
F
|
*
|
*
|
|
|
Boundary
|
T
|
*
|
*
|
|
|
Exterior
|
*
|
*
|
*
|
Table 49. Matrix for ST_Touches (3)
|
|
|
b
|
|
|
|
|
|
Interior
|
Boundary
|
Exterior
|
|
a
|
Interior
|
F
|
*
|
*
|
|
|
Boundary
|
*
|
T
|
*
|
|
|
Exterior
|
*
|
*
|
*
|
For more information, see ST_Touches.
ST_Overlaps compares two geometries of the same dimension. It returns 1 (TRUE) if their intersection set results in a geometry different from both, but that has the same dimension.
 |
The pattern matrix in Table 50 applies to polygon/polygon, multipoint/multipoint and
multipolygon/multipolygon overlays. For these combinations the overlay
predicate returns TRUE if the interior of both geometries intersect the others
interior and exterior.
Table 50. Matrix for ST_Overlaps (1)
|
|
|
b
|
|
|
|
|
|
Interior
|
Boundary
|
Exterior
|
|
a
|
Interior
|
T
|
*
|
T
|
|
|
Boundary
|
*
|
*
|
*
|
|
|
Exterior
|
T
|
*
|
*
|
The pattern matrix in Table 51 applies to linestring/linestring and
multilinestring/multilinestring overlays. In this case the intersection
of the geometries must result in a geometry that has a dimension of 1 (another
linestring). If the dimension of the intersection of the interiors is
1, the ST_Overlaps predicate would return FALSE, however the ST_Crosses
predicate would return TRUE.
Table 51. Matrix for ST_Overlaps (2)
|
|
|
b
|
|
|
|
|
|
Interior
|
Boundary
|
Exterior
|
|
a
|
Interior
|
1
|
*
|
T
|
|
|
Boundary
|
*
|
*
|
*
|
|
|
Exterior
|
T
|
*
|
*
|
For more information, see ST_Overlaps.
ST_Crosses returns 1 (TRUE) if the intersection results in a geometry whose dimension is one less than the maximum dimension of the two source geometries and the intersection set is interior to both source geometries. ST_Crosses returns 1 (TRUE) for only multipoint/polygon, multipoint/linestring, linestring/linestring, linestring/polygon, and linestring/multipolygon comparisons.
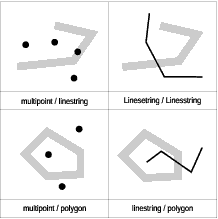 |
The pattern matrix in Table 52 applies to multipoint/linestring,
multipoint/multilinestring, multipoint/polygon, multipoint/multipolygon,
linestring/polygon, linestring/multipolygon. The matrix states that the
interiors must intersect and that the interior of the primary (geometry
a ) must intersect the exterior of the secondary (geometry
b ).
Table 52. Matrix for ST_Crosses (1)
|
|
|
b
|
|
|
|
|
|
Interior
|
Boundary
|
Exterior
|
|
a
|
Interior
|
T
|
*
|
T
|
|
|
Boundary
|
*
|
*
|
*
|
|
|
Exterior
|
*
|
*
|
*
|
The pattern matrix in Table 53 applies to the linestring/linestring,
linestring/multilinestring and multilinestring/multilinestring. The
matrix states that the dimension of the intersection of the interiors must be
0 (intersect at a point). If the dimension of this intersection is 1
(intersect at a linestring), the ST_Crosses predicate returns FALSE;
however, the ST_Overlaps predicate returns TRUE.
Table 53. Matrix for ST_Crosses (2)
|
|
|
b
|
|
|
|
|
|
Interior
|
Boundary
|
Exterior
|
|
a
|
Interior
|
0
|
*
|
*
|
|
|
Boundary
|
*
|
*
|
*
|
|
|
Exterior
|
*
|
*
|
*
|
For more information, see ST_Crosses.
ST_Within returns 1 (TRUE) if the first geometry is completely within the second geometry. ST_Within returns the exact opposite result of ST_Contains.
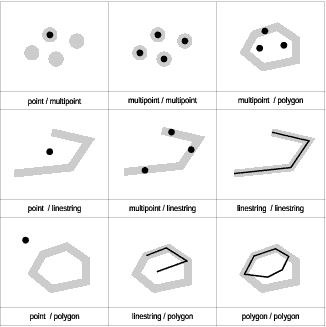 |
The ST_Within predicate pattern matrix states that the interiors of both
geometries must intersect, and that the interior and boundary of the primary
geometry (geometry a ) must not intersect the exterior of the
secondary (geometry b ).
Table 54. Matrix for ST_Within
|
|
|
b
|
|
|
|
|
|
Interior
|
Boundary
|
Exterior
|
|
a
|
Interior
|
T
|
*
|
F
|
|
|
Boundary
|
*
|
*
|
F
|
|
|
Exterior
|
*
|
*
|
*
|
For more information, see ST_Within.
ST_Contains returns 1 (TRUE) if the second geometry is completely contained by the first geometry. The ST_Contains predicate returns the exact opposite result of the ST_Within predicate.
 |
The pattern matrix of the ST_Contains predicate states that the
interiors of both geometries must intersect and that the interior and boundary
of the secondary (geometry b ) must not intersect the exterior of
the primary (geometry a ).
Table 55. Matrix for ST_Contains
|
|
|
b
|
|
|
|
|
|
Interior
|
Boundary
|
Exterior
|
|
a
|
Interior
|
T
|
*
|
*
|
|
|
Boundary
|
*
|
*
|
*
|
|
|
Exterior
|
F
|
F
|
*
|
For more information, see ST_Contains.
The ST_Relate function compares two geometries and returns 1 (TRUE) if the geometries meet the conditions specified by the DE-91M pattern matrix string; otherwise, the function returns 0 (FALSE). For more information, see ST_Relate.
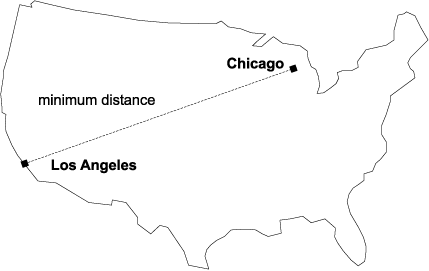
The ST_Distance function reports the minimum distance separating two disjoint features. If the features are not disjoint, the function will report a 0 minimum distance.
For example, ST_Distance could report the shortest distance an aircraft must travel between two locations. Figure 20 illustrates this information.
Figure 20. Minimum distance between two cities. ST_Distance can take the coordinates for the locations of Los Angeles and Chicago as input, and return a value denoting the minimum distance between these locations.
 |
For more information, see ST_Distance.
DB2 Spatial Extender provides predicates and transformation functions that generate new geometries from existing ones.
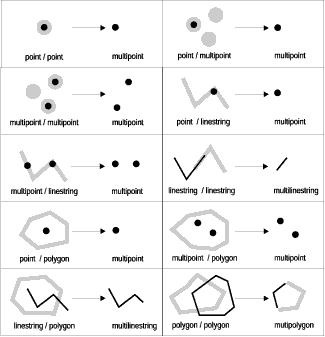
The ST_Intersection function returns the intersection set of two geometries. The intersection set is always returned as a collection that is the minimum dimension of the source geometries. For example, for a linestring that intersects a polygon, the intersection function returns a multilinestring comprised of that portion of the linestring common to the interior and boundary of the polygon. The multilinestring contains more than one linestring if the source linestring intersects the polygon with two or more discontinuous segments. If the geometries do not intersect or if the intersection results in a dimension less that both of the source geometries, an empty geometry is returned.
Figure 21. ST_Intersection. Examples of the ST_Intersection function.
 |
For more information, see ST_Intersection.
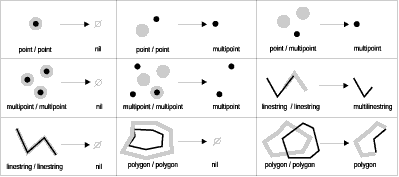
The ST_Difference function returns the portion of the primary geometry that is not intersected by the secondary geometry. This is the logical AND NOT of space. The ST_Difference function operates only on geometries of like dimension and returns a collection that has the same dimension as the source geometries. In the event that the source geometries are equal, an empty geometry is returned.
 |
For more information, see ST_Difference.
The ST_Union function returns the union set of two geometries. This is the logical OR of space. The source geometries must be of like dimension. ST_Union always returns the result as a collection.
 |
For more information, see ST_Union.
The ST_Buffer function generates a geometry by encircling a geometry at a specified distance. A polygon results when a primary geometry is buffered or whenever the elements of a collection are close enough such that all of the buffer polygons overlap. However, when there is enough separation between the elements of a buffered collection, individual buffer polygons will result, in which case the ST_Buffer function returns a multipolygon.
 |
The ST_Buffer function accepts both positive and negative distance, however, only geometries with a dimension of two (polygons and multipolygons) apply a negative buffer. The absolute value of the buffer distance is used whenever the dimension of the source geometry is less than 2 (all geometries that are not polygon or multipolygon).
In general, for exterior rings, positive buffer distances generate polygon rings that are away from the center of the source geometry; negative buffer distances generate polygon or multipolygon rings toward the center. For interior rings of a polygon or multipolygon, a positive buffer distance generates a buffer ring toward the center, and a negative buffer distance generates a buffer ring away from the center.
The buffering process merges polygons that overlap. Negative distances greater than one half the maximum interior width of a polygon result in an empty geometry.
For more information, see ST_Buffer.
For geometries that have measures, the location of a particular measure can be found with the LocateAlong function. LocateAlong returns the location as a multipoint. If the source geometry's dimension is 0 (for example, a point and a multipoint), an exact match is required, and those points having a matching measure value are returned as a multipoint. However, for source geometries whose dimension is greater than 0, the location is interpolated. For example, if the measure value entered is 5.5 and the measures on vertices of a linestring are a respective 3, 4, 5, 6, and 7, the interpolated point that falls exactly halfway between the vertices with measure values 5 and 6 is returned.
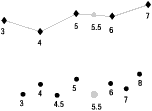 |
For more information, see LocateAlong.
The LocateBetween function returns either the set of paths or locations that lie between two measure values from a source geometry that has measures. If the source geometry's dimension is 0, LocateBetween returns a multipoint containing all points whose measures lie between the two source measures. For source geometries whose dimension is greater than 0, LocateBetween returns a multilinestring if a path can be interpolated; otherwise LocateBetween returns a multipoint containing the point locations. An empty point is returned whenever LocateBetween cannot interpolate a path or find a location between the measures. LocateBetween performs an inclusive search of the geometries; therefore the geometries' measures must be greater than or equal to the from measure and less than or equal to the to measure.
![[Figure]](djxs1019.gif) |
For more information, see LocateBetween.
The ST_ConvexHull function returns the convex hull polygon of any geometry that has at least three vertices forming a convex. If vertices of the geometry do not form a convex, ST_ConvexHull returns a null. ST_ConvexHull is often the first step in tessellation used to create a TIN network from a set of points.
 |
For more information, see ST_ConvexHull.
Generates a polygon from a linestring. For more information, see ST_Polygon.
DB2 Spatial Extender supports three GIS data exchange formats:
DB2 Spatial Extender has several functions that generate geometries from text descriptions.
The text representation is an ASCII string. It permits geometry to be exchanged in ASCII text form. These functions do not require the definition of any special program structures to map a binary representation. So, they can be used in either a 3GL or 4GL program.
The ST_AsText function converts an existing geometry value into text representation. For more information, see ST_AsText.
For a detailed description of well-known text representations, see The OGC well-known text representations.
The DB2 Spatial Extender has several functions that generate geometries from well-known binary (WKB) representations.
The well-known binary representation is a contiguous stream of bytes. It permits geometry to be exchanged between an ODBC client and an SQL database in binary form. These geometry functions require the definition of C structures to map the binary representation. So, they are intended for use within a 3GL program, and are not suited to a 4GL environment.
The ST_AsBinary function converts an existing geometry value into well-known binary representation. For more information, see ST_AsBinary.
For a detailed description of well-known binary representations, see The OGC well-known binary (WKB) representations.
DB2 Spatial Extender has several functions that generate geometries from an ESRI shape representation. The ESRI shape representation supports Z coordinates and measures in addition to the two-dimensional representations supported by the text and well-known binary representations.
The general syntax of these functions is the same. The first argument is the shape representation that is entered as a BLOB data type. The second argument is the spatial reference identifier that will be assigned to the geometry. For example, the GeometryFromShape function has the following syntax:
GeometryFromShape(shapegeometry, SRID)
To map the binary representation, these shape functions require the definition of a C structures. So, they are intended for use within a 3GL program, and are not suited to a 4GL environment.
The AsBinaryShape function converts a geometry value into an ESRI shape representation. For more information, see AsBinaryShape.
For a detailed description of shape representations, see The ESRI shape representations.